Giáo án Hình học Lớp 8 - Tiết 21+22: Ôn tập chương I - Năm học 2020-2021 - Trường THCS Sơn Tiến

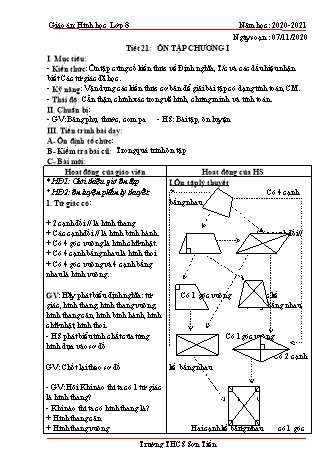
 Giáo án: Hình học Lớp 8 Năm học: 2020-2021
 Ngày soạn : 07/11/2020
 Tiết 21: ÔN TẬP CHƯƠNG I
I. Mục tiêu:
- Kiến thức: Ôn tập củng cố kiến thức về Định nghĩa, T/c và các dấu hiệu nhận 
biết Các tứ giác đã học.
- Kỹ năng: Vận dụng các kiến thức cơ bản để giải bài tập có dạng tính toán, CM.
- Thái độ: Cẩn thận, chính xác trong vẽ hình, chứng minh và tính toán.
II. Chuẩn bị: 
- GV: Bảng phụ, thước, com pa - HS: Bài tập, ôn luyện
III. Tiến trình bài dạy:
A- Ôn định tổ chức:
B- Kiểm tra bài cũ: Trong quá trình ôn tập
C- Bài mới:
 Hoạt động của giáo viên Hoạt động của HS 
* HĐ1: Giới thiệu giờ ôn tập I.Ôn tập lý thuyết
* HĐ2: ôn luyện phần lý thuyết Có 4 cạnh 
1. Tứ giác có: bằng nhau
+ 2 cạnh đối // là hình thang
+ Các cạnh đối // là hình bình hành. 2 cạnh// Các cạnh đối//
+ Có 4 góc vuông là hình chữ nhật. 
+ Có 4 cạnh bằng nhau là hình thoi
+ Có 4 góc vuông và 4 cạnh bằng 
nhau là hình vuông.
GV: Hãy phát biểu định nghĩa: tứ Có 1 góc vuông hai góc kề
giác, hình thang, hình thang vuông, Một đáy bằng nhau
hình thang cân, hình bình hành, hình 
chữ nhật, hình thoi.
- HS phát biểu tính chất của từng Có 1góc vuông
hình dựa vào sơ đồ
 Có 2 cạnh 
GV: Chốt lại theo sơ đồ kề bằng nhau
- GV: Hỏi Khi nào thì ta có 1 tứ giác 
là hình thang? / \
- Khi nào thì ta có hình thang là?
+ Hình thang cân
+ Hình thang vuông Hai cạnh kề bằng \ nhau / có 1 góc 
 Trường THCS Sơn Tiến Giáo án: Hình học Lớp 8 Năm học: 2020-2021
+ Hình bình hành vuông
- Khi nào ta có tứ giác là hình bình 3. Dấu hiệu nhận biết các loại tứ giác
hành? ( 5 trường hợp) II. Bài tập áp dụng
- Khi nào ta có HBH là:
+ Hình chữ nhật Chữa bài 88/SGK
+ Hình thoi ABCD; E, F, G, H là
- Khi nào ta có HCN là hình vuông? GT trung điểm của AB, BC, CD, DA
Khi nào ta có hình thoi là h vuông ? KL Tìm đk của AC & BD để EFGH là
- Để EFGH là HCN cần có thêm đk a) HCN
gì ? b) Hình thoi
- HS đọc đề bài & vẽ hình, ghi gt, kl c) Hình vuông
 B Chứng minh:
 E F Ta có: E, F, G, H theo thứ tự là trung điểm 
 A C của AB, BC, CD & DA ( gt) nên:
 1
 H G EF // AC & EF = AC EF // GH
 2
 D 1
- GV: Để cm AEBM là hình thoi có GH // AC & GH = AC và EF = GH
thể cm: 4 cạnh của nó bằng nhau: 2
 Vậy EFGH là hình bình hành
+ AEBM là hình vuông khi có ·AMB 
 a) Hình chữ nhật: EFGH là HCN khi có 1 
= 900
 góc vuông hay EF//EH
muốn vậy AM phải vừa là trung 
 Mà EF  EH
tuyến vừa là đường cao ABC 
 Vậy khi AC  BD thì EFGH là HCN
phải là vuông cân.
 b) EFGH là hình thoi khi EF = EH mà ta 
 1 1
 biết EF AC ; EH = BD do đó khi 
 2 2
 AC = BD thì EF = EH
 Vậy khi AC = BD thì EFGH là hình thoi
 c) EFGH là hình vuông khi EF  EH & 
 EF = EH theo a & b ta có AC  BD thì 
 EF  EH 
 AC = BD thì EF = EH
 Vậy khi AC  BD & AC = BD thì EFGH 
 là hình vuông
D- Luyên tập - Củng cố:
- Trả lời bt 90/112: + Hình 110 có 2 trục đx & 1 tâm đx
 + Hình 111 có 2 trục đx & 1 tâm đx.
E- BT - Hướng dẫn về nhà:
- Làm bài 87 (SGK) - Ôn lại toàn bộ chương
 Trường THCS Sơn Tiến Giáo án: Hình học Lớp 8 Năm học: 2020-2021
 Ngày soạn : 14/11/2020
 Tiết 22: ÔN TẬP CHƯƠNG I (TT)
I. Mục tiêu:
- Kiến thức: Ôn tập củng cố kiến thức về định nghĩa, tính chất và các dấu hiệu 
nhận biết tứ giác là hình bình hành, hình chữ nhật, hình thoi, hình vuông.
- Kỹ năng: Vận dụng các kiến thức cơ bản để giải bài tập có dạng tính toán, chứng 
minh các hình. HS thấy được mối quan hệ giữa các tứ giác đã học dễ nhớ & có thể 
suy luận ra các tính chất của mỗi loại tứ giác khi cần thiết
- Thái độ: Cẩn thận, chính xác trong vẽ hình, chứng minh và tính toán.
II. Chuẩn bị: 
- GV: Bảng phụ, thước, com pa - HS: Bài tập, ôn luyện
III. Tiến trình bài dạy:
A- Ôn định tổ chức:
B- Kiểm tra bài cũ: Trong quá trình ôn tập
C- Bài mới:
 Hoạt động của giáo viên Hoạt động của HS 
1. Câu hỏi trắc nghiệm
Câu 1: Cho hình bình hành MNPQ 1. Câu hỏi trắc nghiệm
biết góc N = 600. Khi đó: Học sinh vẽ hình vào vở nháp sau đó lựa 
 ^ ^
a. M 600 b. Q 600 chọn đáp án đúng
 ^ ^ Câu 1: Đáp án b.
c. Q 1200 d. P 600 
Câu 2: Những tứ giác đặc biệt nào có 
hai đường chéo bằng nhau: Câu 2: Đáp án d.
a. Hình chữ nhật 
b. Hình bình hành 
c. Hình thang cân 
d. Cả a và c
Câu 3: Tam giác ABC có trung tuyến Câu 3: Đáp án b.
BM = 3cm; AC = 6cm. Ta có tam 
giác ABC vuông tại: 
a. A b. B c. C d. D 
2. Bài tập tự luận 2. Bài tập tự luận
Bài 89: SGK B Bài 89: SGK
GV: Vẽ hình C/m:
 j
 M a) D, M thứ tự là trung điểm của AB, AC 
 E
 D nên ta có DM là đường trung bình của 
 tam giác ABC DM // AC
 A C AC  AB ( gt) mà DM // AC DM  AB 
 Trường THCS Sơn Tiến
 B
 B
 j
 M
 E j
 D M
 E
 D
 A C
 A C Giáo án: Hình học Lớp 8 Năm học: 2020-2021
HS: Thực hiện (1)
GV. Để chứng minh E đx M qua AB Ta có: E đx với M qua D do đó ED = DM 
ta làm thế nào? (2)
HS. Trả lời Vậy từ (1) và (2) AB là đường trung 
 trực của đoạn thẳng EM hay E đx M qua 
 AB.
 b) AB và EM vuông góc với nhau tại trung 
GV: AEMC, AEMB là hình gì? Vì điểm của mỗi đường nên AEBM là hình 
sao? thoi 
HS. Trả lời Ta có : AE // BM (cmt) AE // MC
GV: Nêu cách tính chu vi của hình ta lại có EM // AC (cmt)
thoi? Vậy AEMC là hình bình hành
HS: Suy nghĩ, trả lời c) AM = AE = EB = BM = BC = 2 cm
 2
GV: Hình thoi AEBM là hình vuông Chu vi hình thoi EBMA = 4.2 = 8 cm
khi t/m thêm đk gì? d. Hình thoi AEBM là hình vuông 
HS: Suy nghĩ, trả lời A· MB = 900 AM vừa là trung tuyến vừa 
 là đường cao ABC phải là tam giác 
Bài toán: Cho hình bình hành vuông cân tại A.
ABCD. Gọi H và K lần lượt là hình Bài toán: 
chiếu của A và C trên đường chéo a) Xét tứ giác AHCK có AH  BD và 
BD. CK  BD => AH // CK
a) Chứng minh rằng AHCK là hình xét AHD và CKB có : Hµ Kµ 900
bình hành. AD = BC và ·ADH C· BK
 b) Gọi O là trung điểm của HK. Suy ra AHD = CKB (cạnh huyền - 
Chứng minh rằng ba điểm A, O, C góc nhọn)=> AH = CK 
thẳng hàng
 A B Vậy Tứ giác AHCK là hình bình hành
 b) Xét hình bình hành AHCK, trung điểm 
 K
 O của đường chéo HK cũng là trung điểm 
 O của đường chéo AC ( tính chất đường chéo 
 H
 hình bình hành). Do đó ba điểm A, O , C 
 D C thẳng hàng
D- Luyên tập - Củng cố:
 - Nêu định nghĩa và tính chất của các loại hình đã học.
 - Nêu các cách để chứng minh các loại hình đó.
E- BT - Hướng dẫn về nhà:
- các bài còn lại trong SGK và xem lại các bài đã chữa
- Ôn lại toàn bộ lý thuyết của chương.
- Chuẩn bị tốt cho thi khảo sát giữa kì I.
 Trường THCS Sơn Tiến
 B
 j
 M
 E
 D
 A C Giáo án: Hình học Lớp 8 Năm học: 2020-2021
 Trường THCS Sơn Tiến